Guías matemáticas 6°
Copiar,estudiar,realizar los talleres propuestos.
OPERACIONES ENTRE CONJUNTOS
Unión de conjuntos:
Al realizar esta operación estamos conformando un nuevo conjunto, que se llama conjunto solución, que contiene todos los elementos o miembros de los conjuntos que se estén uniendo, sin que ninguno de sus miembros se repita en el conjunto solución. Por ejemplo:
Dados: A = {-1, 1, 2, 3} B = {2, 4, 6} C= {4, 5, 7, 8}
A U B = {-1, 1, 2, 3, 4, 6}
Observe que el resultado A U B no contiene elementos repetidos
A U B U C = {-1, 1, 2, 3, 4, 5, 6, 7, 8}
Intersección de conjuntos:
Esta operación entre conjuntos conforma un nuevo conjunto que contenga los elementos o miembros comunes a los conjuntos que hagan parte de esta operación. Por ejemplo si consideramos los conjuntos A, B y C arriba mencionados, al operar; se obtiene:
A n B = {2}

B n C = {4}
A n B n C = { } Puesto que no hay ningún elemento que esté en los tres conjuntos.
(A U B) n C Observe que en este ejemplo se está aplicando la propiedad asociativa para la operación de unión entre A y B y a su resultado hacer la intersección con C.
(A U B) n C = {4}
Diferencia de conjuntos:
Cuando se analiza la diferencia entre A y B, se obtiene como respuesta exclusivamente los elementos del conjunto A que no estén en el conjunto B.
Por ejemplo si consideramos los conjuntos A, B, C que aparecen arriba:
A - B = {-1, 1, 3}
B - C = {2, 6}
B - A = {4, 6}
C - B = {5, 7, 8}
Complemento de un conjunto:
Se buscan todos los elementos que le hagan falta a un conjunto para convertirse o ser el conjunto universal o referencial. Por ejemplo:
A´= {4, 5, 6, 7}
B´= {-1, 1, 3, 5, 7, 8}
C´= {-1, 1, 2, 3, 6,}
(A U B)´= {5, 7, 8}
Diferencia simétrica de conjuntos:
Se presenta cuando se consideran todos los elementos que sólo pertenecen los conjuntos, sin tener en cuenta lo que tienen en común. En otras palabras, en la diferencia simétrica no se tiene en cuenta ningún elemento de la intersección entre los conjuntos, los demás sí. Por ejemplo, dados los conjuntos
A = {-1, 1, 2, 3,} B = {2, 4, 6} C = {4, 5, 7, 8}
y U = {-1, 1, 2, 3, 4, 5, 6, 7, 8} (Conjunto Universal o referencial)
![]()
OPERACIONES DE CONJUNTOS
Dados los siguientes conjuntos, indique qué elementos forman la solución.
|
U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 15 } |
|
|
A = { 4, 8, 10, 12 } |
B = { 3, 6, 9, 12, 15 } |
|
C = { 1, 2, 3, 11, 12, 13 } |
D = { 1, 5, 6, 10, 11 } |
| E = { 12,13,14,15} | |
|
a) A u B |
b) (A n B)´ |
c) (D n E) – A |
|
d) B u C |
e) A´ |
f) B´ |
|
g) E´ n D |
h) B n E |
i) B u E |
|
j) A u C |
k) ( B u C)´ |
l) ( C n D )´ |
|
m) ( A n D )´ |
n) ( E u C )´ |
|
Números primos
Un número primo es un número entero mayor que cero, que tiene exactamente dos divisores positivos. También podemos definirlo como aquel número entero positivo que no puede expresarse como producto de dos números enteros positivos más pequeños que él, o bien, como producto de dos enteros positivos de más de una forma. Conviene observar que con cualquiera de las dos definiciones el 1 queda excluido del conjunto de los números primos.
Ejemplos:
a) El 7 es primo. Sus únicos divisores son 1 y 7. Sólo puede expresarse como producto de 7·1.
b) El 15 no es primo. Sus divisores son 1, 3, 5 y 15. Puede expresarse como 3·5.
( y también como 15·1)
El término primo no significa que sean parientes de alguien. Deriva del latín "primus" que significa primero (protos en griego). El teorema fundamental de la aritmética afirma que todo número entero se expresa de forma única como producto de números primos. Por eso se les considera los "primeros", porque a partir de ellos obtenemos todos los demás números enteros. (El 15 se obtiene multiplicando los primos 3 y 5)
Los 25 primeros números primos son 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97, que son todos los primos menores que 100.En la siguiente tabla tenemos todos los primos menores que 1000, que hacen un total de 168 (21×8)
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
61 |
67 |
71 |
73 |
|
79 |
83 |
89 |
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
179 |
181 |
|
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
269 |
271 |
277 |
281 |
283 |
293 |
307 |
|
311 |
313 |
317 |
331 |
337 |
347 |
349 |
353 |
359 |
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
419 |
421 |
431 |
433 |
|
439 |
443 |
449 |
457 |
461 |
463 |
467 |
479 |
487 |
491 |
499 |
503 |
509 |
521 |
523 |
541 |
547 |
557 |
563 |
569 |
571 |
|
577 |
587 |
593 |
599 |
601 |
607 |
613 |
617 |
619 |
631 |
641 |
643 |
647 |
653 |
659 |
661 |
673 |
677 |
683 |
691 |
701 |
|
709 |
719 |
727 |
733 |
739 |
743 |
751 |
757 |
761 |
769 |
773 |
787 |
797 |
809 |
811 |
821 |
823 |
827 |
829 |
839 |
853 |
|
857 |
859 |
863 |
877 |
881 |
883 |
887 |
907 |
911 |
919 |
929 |
937 |
941 |
947 |
953 |
967 |
971 |
977 |
983 |
991 |
997 |
¿Cómo averiguamos si un número es primo?
Para averiguar si un número es primo, se divide entre los primeros números primos, hasta que el cociente sea igual o menor que el divisor. Si todas las divisiones son enteras, es un número primo.
Números compuestos
Un número compuesto es el que posee más de dos divisores. Es decir, aquel que se puede dividir por sí mismo, por la unidad y por otros números.
Ejemplo:
12, 72, 144, ...
Los números compuestos se pueden expresar como productos de potencias de números primos. A dicha expresión se le llama descomposición de un número en factores primos.
Ejemplo:
70 = 2 · 5 · 7
Factorizar un número
Para factorizar un número o descomponerlo en factores efectuamos sucesivas divisiones entre sus divisores primos hasta obtener un 1 como cociente.
Para realizar las divisiones utilizaremos una barra vertical, a la derecha escribimos los divisores primos y a la izquierda los cocientes.
Ejemplo:

Solución: 432 = 24 · 33
EL MAXIMO COMUN DIVISOR (M.C.D) :
El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el M.C.D.
Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos.

El MCD son los factores comunes con su menor exponente, esto es: mcd= 2^2x3=12
EL MINIMO COMÚN MULTIPLO ( m.c.m):
Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el m.c.m de 72 y 50 será:

Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:
mcm= 2^3x5^2x3^2=1800
Segunda Forma de Hallar el m.c.m.
Se puede utilizar la descomposición en factores primos de un número para encontrar el m.c.m. de varios números. Veamos:
Calculemos el Mínimo Común Múltiplo de (8, 12, 15)
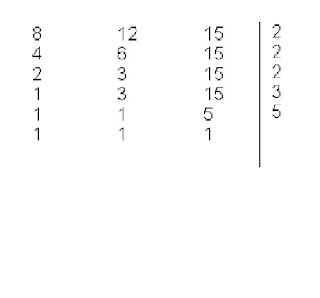
Solución:
1. Procedemos primero a sacar mitad de los números mencionados en este caso solo tienen 8 y 12, como el 15 no tiene mitad exacta entonces lo que hacemos es bajar el número igual.(Renglón 2).
2. Repetimos el procedimiento hasta que algún número ya no tenga mitad.
3. Posteriormente se procede a sacar tercera, quinta o lo que tengan hasta que aparezca 1 en cada uno de los números.
4. El m.c.m. se obtendrá multiplicando los números que están en la derecha de la línea vertical, para nuestro ejemplo serian 2x2x2x3x5 =120. Por lo tanto m.c.m. (8, 12, 15)= 120
Calculemos el Mínimo Común Múltiplo de (90, 54, 72)

El m.c.m. se obtendrá multiplicando los números que están en la derecha, para nuestro ejemplo serian 2x2x2x3x3x3x5 =1080 Por lo tanto m.c.m. (90, 54, 72)= 1080
TALLER
Ejercicios: Calcular el M.C.D y m.c.m. de:
a) (7, 11, 15)
b) (7, 9, 13)
c) (3, 8, 14)
d) (4, 7, 18)
e) (26 y 65)
f) (90 y 154)
g) (8 y 10)
h) (12 y 14)
i) (15 y 42)
j) (84 y 90)
|
|
INSTITUCIÓN EDUCATIVA COMERCIAL ENVIGADO
|
CÓDIGO |
|
PRÁCTICAS PEDAGÓGICAS |
VERSIÓN: |
|
|
Taller para preparación evaluación |
PÁG. 1 |
REPASAR LOS Criterios de divisibilidad
Para saber si un número es divisible por algún otro número
Utilizamos los llamados criterios de divisibilidad. Son estos:
Ø Divisibilidad por 2: un número es divisible por dos si termina en
cero o en cifra par.
Ø Divisibilidad por 3: un número es divisible por tres, si la suma de
sus cifras es múltiplo de tres.
Ø Divisibilidad por 4: las dos últimas cifras tienen que ser dos ceros
o un número múltiplo de 4.
Ø Divisibilidad por 5: un número es divisible por cinco cuando acaba
en cero o en cinco.
Ø Divisibilidad por 6: tiene que ser divisible por 2 y por 3.
Ø Divisibilidad por 9: un número es divisible por nueve cuando la suma
de sus cifras es múltiplo de nueve.
Ø Divisibilidad por 10: tiene que terminar en cero. de manera similar,
si termina en 00 es divisible por 100; si termina en 000 es divisible
por 1000.
Ø Divisibilidad por 11: un número es divisible por once cuando la
diferencia entre la suma de las cifras que ocupa la posición par y la
suma de las cifras que ocupan la posición impar son múltiplo de once.
Ø Divisibilidad por 100: un número es divisible por cien cuando las
dos últimas cifras son 00.
Taller de preparación para la prueba de tercer periodo
1.- Calcula 4 múltiplos de cada uno de las siguientes cifras:
3 8 5 2 10 15
2.- Escribe 3 divisores de cada uno de los siguientes números:
12 20 14 30 45 60
3.- Define qué es un número primo. Escribe 5 números primos.
4.- Define qué es un número compuesto. Escribe 5 números compuestos.
5.- Los criterios de divisibilidad nos sirven para saber si un número se puede dividir por otro. Sabiendo esto, señala porqué números son
divisibles las siguientes cantidades:
El 24 por ejemplo: es divisible por 1, 24, 2, 3, 4 y 6.
35 120 66 75 49 63
23 98 18 76 300 102
6.- Descomponer estos números en factores primos.
15 18 42 55 70 26
84 124 95 35 100 36
7.- Calcula el M.C.D. y el M.C.M. de los siguientes números:
4 y 6 20 y 30 4 y 8 12 y 24
12 y 19 72 y 84 90 y 120 24 y 50
8.- Entre los números dados uno no es primo ¿Cuál es?
169, 277, 563, 971
9.- Dado el número 887, muestra tres de sus divisores que no sean ni 887 ni 1.
10.- Dado el número 30, muestra tres de sus múltiplos mayores que 113.
11.- Usando los criterios de divisibilidad, el número 642 es divisible por:
2, 3, 4, 5, 6, 11, ninguno de los anteriores.
12.-Problemas M.C.D (Realiza los procedimientos)
Ø Tres cables que miden 20, 150 y 180 metros se dividen en el menor número de trozos de igual longitud. ¿Cuál es la longitud de cada trozo?
A. 5m B. 20m C.15m D. 10m
Ø Un albañil debe colocar losetas cuadradas en un piso de un baño cuyas dimensiones son 270 cm y 300 cm. ¿Cuántas losetas enteras entrarán en dicho piso, si estas deben ser del mayor tamaño posible?
A. 30 B. 90 C. 10 D. 19
Ø Juan tiene un terreno de forma rectangular de 40m de ancho y 96m de largo. si se divide su terreno en parcelas cuadradas iguales y planta en el interior de cada parcela 3 árboles, ¿cuál es el mínimo número de árboles que podría sembrar en todo su terreno? M.C.D
A. 160 B.150 C. 190 D. 180
13.- Problemas de M.C.M (Realiza los procedimientos)
Ø Cuatro ciclistas compiten en una pista circular y la recorren totalmente en 8, 10, 12 y 15 segundos, respectivamente. Si parten juntos, ¿en cuántos minutos se encontraran en la partida?
A. 120 B.1 C. 2 D. 3
Ø Un vendedor tiene entre 600 y 800 naranjas. Si se puede agruparlas de 15 en 15, de 18 en 18 y de 24 en 24 sin que sobre alguna, ¿cuántas naranjas tiene el vendedor?
A. 640 B.720 C.760 D.800
Ø Se compran televisores de 17 pulgadas a 3 por 1200 dólares y se venden a 4 por 2400 dólares. Para ganar 3000 dólares, ¿cuántos se debe vender?
A. 15 B. 12 C. 8 D.10
PARA LA EVALUACIÓN DEL TERCER PERIODO DEBES TENER EN CUENTA
Estudiar los temas de:
Ø Criterios de divisibilidad.
Ø Potenciación y sus propiedades, ejemplos. (Ver cuaderno matemáticas – Repaso)
Ø Radicación ,ejemplos (Ver cuaderno matemáticas – Repaso)
Ø Documento números primos y compuestos. (Ver página internet: matemagica2.webnode.es). (cuaderno matemáticas).
Ø Máximo Común Divisor M.C.D y Mínimo Común Múltiplo M.C.M.
Ø Problemas de M.C.D y M.C.M (Ver Video)
Ø Proposiciones lógicas y conjuntos.(Ver página internet : matemagica2.webnode.es)
Ø Guías Geometría: Unidades de medida de longitud, superficie, volumen, Áreas y perímetro de figuras planas. .(Ver página internet : matemagica2.webnode.es)
Ø Guías Estadística: Medidas de tendencia central como: Media o promedio, Moda,
Ø Mediana. .(Ver página internet : matemagica2.webnode.es).
Ø Realiza y entrega este taller el día lunes 12 de agosto en hojas de block.
Nota: Aprovecha el tiempo y estudia con dedicación.
FRACCIONES Y SUS OPERACIONES
COPIA EN GOOGLE PARA ESTUDIAR:
https://www.google.com.co/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&docid=j7AcTgEE3YVOfM&tbnid=inb4mwNWIxFTqM:&ved=0CAUQjRw&url=http%3A%2F%2Fwww.slideshare.net%2FJulio1960%2Fejercicios-de-fracciones-soluciones-6&ei=4pttUvaZK9OpkAfv2oDIAQ&bvm=bv.55123115,d.eW0&psig=AFQjCNFf0XSc54l8pkBkYf2agws7Th7ogg&ust=1383000873490597
VER VIDEO DE TRONCHO Y PONCHO SOBRE FRACCIONES.
REALIZA EL TALLER PROPUESTO EN CLASE.
LA EVALUACION ES 28 DE OCTUBRE DE 2013.

